機械学習は、AIの開発や活用をするにあたり必ず理解しておかなければならない知識です。機械学習なしにAIを扱うエンジニアにはなれないと言っても過言ではありません。
この機械学習を理解するためには、前提として数学を知識も必要です。今回は機械学習を学びたい皆さんに向けて、機械学習の基礎となる知識を順を追ってご説明します。
機械学習の定義とは
まずは簡単に機械学習の定義を理解していきましょう。
機械学習とは人工知能(AI)の一種です。AIに明確な定義はなく、数学などの力を使って様々な考えを導いたりタスクをこなしたりするもの全般を指します。
そのAIの一種である機械学習とは与えられたサンプルデータから未知の部分を推測する技術です。
今回は簡単に分からない部分を機械的に推測するものだと理解して以下を読み進めていきましょう。
機械学習で利用されるモデルとは
機械学習には「モデル」と呼ばれる考え方があります。ここでのモデルとは「機械学習によって導く答え」であると考えておきましょう。
機械学習は様々な事柄を数式にして表現する仕組みです。つまり答えとは「機械学習によって導き出された数式」のことを指します。ただ、機械学習で導き出された数式が100%正しいとは言い切れません。誤差を含んでしまうこともあります。機械学習を利用すればどんなものも完璧な数式で表現できるわけではないのです。
数式には様々なものがありますので、実際に機械学習で導き出されるものも多種多様です。ただ、最初から全ての数式のパターンを理解するのは現実的ではありません。そこで今回はイメージしやすいように簡単な数式に絞って詳しくご説明していきます。
機械学習の問題イメージ
それでは機械学習でモデルを導き出す例題を考えてみましょう。まずは以下のグラフをご確認ください。
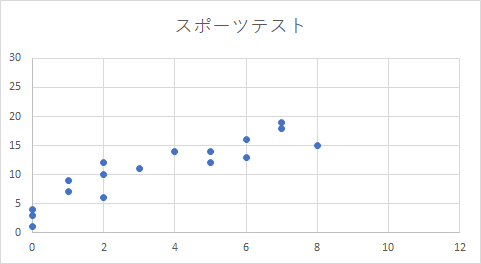
こちらのグラフはいくつものデータを集めてグラフとしてにプロットしたものです。今回はとあるスポーツテストの練習時間と点数の関係をグラフにしています。X軸はテストに向けた練習時間でありY軸がテストの点数です。テストではシュートの成功回数が点数になったとしましょう。
このグラフでは9時間以上テストのために練習をした人がいません。ただ、概ね右肩上がりのグラフですので、練習時間の増加とシュートの成功回数には比例関係があると思われます。そこで「10時間以上練習した場合、どの程度シュートの成功回数が増えるのか」考えてみたくなりました。
以下ではこれを機械学習で考えていく手法についてご説明します。
この問題をどのように解けばよいのか
それではこの問題をどのようにして解けば良いのでしょうか。問題を解くためにまずはモデルを考えます。
今回は上記のグラフから概ね直線であると考えてみましょう。直線だと仮定した場合以下のようなグラフでイメージできます。人によって赤のグラフをイメージすることや緑のグラフをイメージすることがあるでしょう。イメージした直線のことを機械学習ではモデルと呼びます。
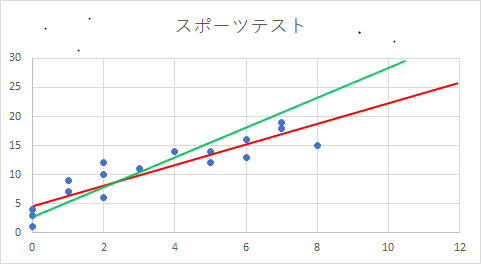
機械学習は上記のようなモデルと呼ばれる数式を考えることが最初のステップです。そこから、具体的にどのような数式であるのかパラメータを決定していきます。
今回は直線の数式を考えましたが、必ずしもこのような数式になるとは限りません。曲線を含んだ難しい関数をイメージしなければならないことも多々あります。ただ、そのような数式は難しいものですので、まずは直線で理解を深めていきましょう。
目的関数を考えて機械学習を進める
上記のような数式を考えた場合、モデルの数式は以下のとおりです。1次関数をイメージすると良いでしょう。
![]()
文字の意味はそれぞれ以下のとおりです。
- x:入力変数
- y:出力変数
- a,b:パラメータ
機械学習では上記のうち「パラメータ」の最適化を目指します。最適化とは関数の値が最小・最大になるパラメーターを見つけ出すことを意味する数学用語です。機械学習での最適化とはモデルが実際のデータの並びに近づくパラメーターを見つけ出すことを指します。上記のグラフであれば、緑色や赤色など考えられるグラフのうち、どれが最適なのかを見つけ出すのです。
最適なパラメーターを見つけ出すためには「目的関数」と呼ばれるものを利用します。以下ではこの考え方についてご説明していきます。
目的関数とは
目的関数とは上記で推測したモデルのパラメーターが最適なものであるか評価するものです。目的関数が示す値は「予測値と実際のデータの差」の合計であり、機械学習で導き出された値とサンプルデータの値にどれだけの誤差があるかを確認できます。
言うまでもなく誤差は小さいに越したことがありません。つまり、高い評価を得られるのは目的関数の値が小さいモデルであり、私たちは目的関数の値が小さくなるパラメーターを探し出す必要があります。
目的関数のパラメーターを評価するためには以下の二つの手法がよく使われます。
- 最小絶対値法
- 最小二乗法
これらの数式で求められる数値をいかに小さくできるかが重要となるのです。以下では具体的に数式を交えてご説明します。
最小二乗法
まずは最小二乗法の公式を確認していきましょう。
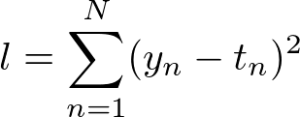
ここでy_nは実際のサンプルデータ、t_nは上記のモデルから算出された対応する数値です。ただ、t_nはモデルの数式にも置き換えられますので以下のとおりとなります。
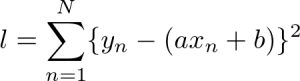
こちらの公式は厳密には最小二乗法と呼ばれるものではなく、二乗誤差関数と呼ばれるものです。二乗誤差関数を利用してパラメーターを評価することを最小二乗法と呼んでいます。
二乗誤差関数ではモデルから算出した値とそれに対応する値の誤差を二乗してその和を求めています。ひとつだけのデータに対して誤差を求めるのではなく、算出されたすべてのデータに対して誤差を算出し総和を求めるのです。モデルのパラメーターは全てのデータに対して適切であることが求められますので、全てのデータに注目して可能な限り誤差が少ないものを求めます。
なお、誤差を二乗するのは値がマイナスになった場合に処理しやすくするためです。可能な限りマイナスを意識せずに処理できるように考えられています。
最小絶対値法
続いて最小絶対値法の公式を確認していきましょう。
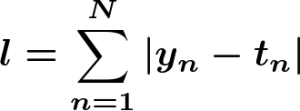
この数式でもy_nとt_nが定められています。t_nはモデルの数式に置き換えられますので以下とおりとなります。
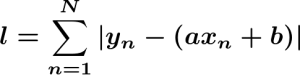
こちらはモデルと対応するデータとの距離を絶対値で算出しその和を求めたものです。純粋に距離を求めているのですが、数式の都合から距離がマイナスになる場合があります。そのまま和を求めると算出される値が不正なものになってしまいますので、絶対値をつけることで距離として正しく扱えるものにしています。
目的関数な考え方は最小二乗法と基本は同じです。モデルとデータの誤差を可能な限り小さくするものです。この点は皆さんも理解していただけることでしょう。
どちらも目的関数には違いありませんが、実際には目的関数として利用されているのは最小二乗法が大半です。理由としては絶対値を用いて計算をするよりも二乗を用いて計算した方がシンプルであるからです。その時々に応じて適切なものを利用すると考えておきましょう。
微分で目的関数の値を最小化する
モデルを評価するために目的関数が役に立つことをご説明しました。可能な限り目的関数の値を小さくすることで、より良いモデルになることは理解いただけたことでしょう。
それでは目的関数の値を可能な限り小さくするにはどうすれば良いのでしょうか。これを実現するためには数学の中でも微分の知識を利用します。以下では自分を利用した目的関数の最小化についてご説明をします。
微分とは~数学のおさらい~
簡単に微分の概要についておさらいをしておきましょう。微分とは高校数学で学ぶ内容であり「グラフの接線の傾き(変化の割合)」を求めるものです。
接線の傾きを求めるものですので、微分は2次関数以上に対して利用できるものです。この点も高校数学で学んだ人が大半のはずです。なんとなくでも微分について思い出しておきましょう。
微分によって極値が求まる
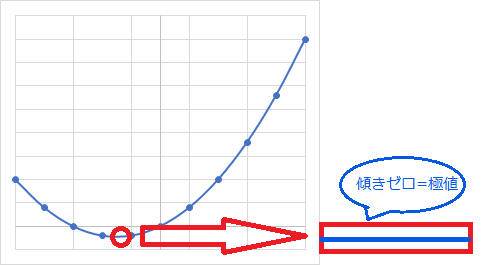
それでは微分とはどのような目的でするものなのでしょうか。これはグラフの最大値や最小値に該当する「極値」を求めるためです。増減表などを用いてグラフの極値を算出しその値を活用していきます。
極値を算出するためにはまず導関数を求めます。導関数の算出方法は割愛しますが、以下に関数f(x)と導関数f‘(x)の例を挙げておきます。
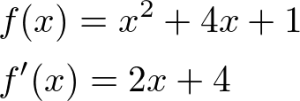
ある関数を微分することによって導関数が求まり、この導関数を用いて極値が求まります。なお極値では導関数の値がゼロになります。つまり傾きがゼロということです。グラフでイメージすると以下のとおりです。
極値の計算から目的関数を最小化する
モデルを最適なものにするためには、上記で算出した目的関数の値を最小化しなければなりません。これが今回私たちがやらなければならないことです。
数値の最小化を実現するためには、上記式のa,bそれぞれに対して極値を求めます。微分して傾きがゼロになる部分が最小値ということです。なお、それぞれの文字に対してを微分をしますので、この場合は偏微分と呼ばれます。偏微分は一旦一つの文字だけに注目しそれ以外の文字は定数として扱う微分の方法です。
傾きがゼロになる部分がモデルのパラメーターとして最も適切だと考えられます。そのためモデルを2次以上の関数として使う場合、接線の傾きを意識してパラメーターの最適化をしなければなりません。
なお、傾きがプラスからマイナス、マイナスからプラスへと変化する過程で極値を通過します。目的関数を最小化する際には、傾きの変化に意識しておくと良いでしょう。
線形代数の活用
線形代数を活用することで複数の入力や複数の接続を同時に扱えるようになります。ひとつのモデルで同時に数値を扱いたい場合は線形代数を使えなければなりません。
例えば商品の販売であれば「気温」「天気」「価格」「時間」など多くの条件(入力)が考えられます。そこから、「Aの販売数」「Bの販売数」など複数の結果(出力)を導きます。このような考えをするにあたり線形代数が必要です。
線形代数と表現すると高校で学ぶ数学ではあまり馴染みがないかもしれません。線形代数は概ね行列であると考えるといいでしょう。ただ、行列の高校で理系のクラスに属していなければ学ばない可能性がある分野です。そのため計算方法などについては別途理解が必要です。
線形代数とは~数学のおさらい~
線形代数は高校数学ではほぼ行列として扱われるものの、大学などでは理系のみならず経済学など文系の学部でも利用されるものです。つまり、それだけ世の中的に馴染みの深いものであり、機械学習においても理解しておかなければならない単元です。
線形代数という言葉は実は「線形」と「代数」に分かれます。それぞれの言葉を理解していくことで線形代数の概要が把握可能です。それぞれを簡単に説明していきます。
まずは代数学について簡単に説明をします。こちらは数字の代わりに文字を利用して計算する手法のことです。例えば中学校の数学では「一個100円のりんごがx個あります」などの問題を解いてきたことでしょう。このように数字だけではなく文字を含んだ計算をすることが代数学です。
ただ、実際にはこれだけではなく、文字の係数に注目をして行列的に扱うこともあります。その例を以下で確認してみましょう。
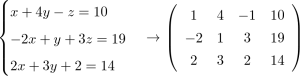
図の左側は中学校などでも目にする連立方程式です。このような問題についても皆さんと解いてきたことでしょう。文字を整理すれば今でも解ける人はいるはずです。ただ、文字の種類が多くなったり連立方程式の数が増えたりすると処理に困ってしまいます。
そこで図の右側のように係数を数字だけで表すようにします。そうすることで数字だけの情報が手に入り、処理がしやすくなります。「文字の取り扱いは!?」と気になる人も多いと思いますが、代数学の概念ですのでその点は無視しましょう。
続いて線形的についても簡単に説明をします。線形的とはイメージを持ちやすくすると直線を取り扱う手法です。皆さんも曲がったものより直線のものの方が計算しやすいイメージがあることでしょう。
ただ、完全にまっすぐのものしか取り扱わないわけではありません。例えば以下を見てみましょう。
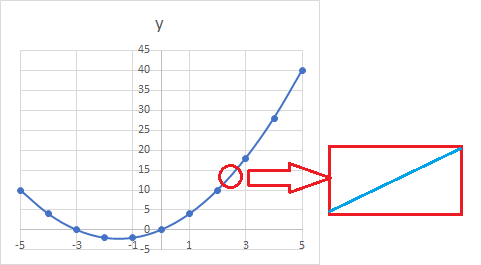
元のグラフは中学校で学ぶ2次関数です。曲線が含まれているグラフですので、皆さんも上手く書くのには苦労したのではないでしょうか。
このグラフは曲線ではあるものの、非常に狭い範囲を拡大して考えてみると直線であると考えられます。これは微分の時と同じ考え方です。つまり、完全に直線であるものだけを取り扱うのではなく、曲線も直線に近似して計算が可能です。数学は様々なところで直線が出てきますので、可能な限り全てを直線に近似して処理をしようという考え方です。
線形代数の利用で複数の情報を扱えるようになる
線形代数を活用することで私たちはn×nの情報を取り扱いやすくなります。複数の入力、出力、パラメーターを同時に扱えるようになることで、より正確なモデルを生み出せるようになります。
同時に扱う入力、出力、パラメーターの数が少ないうちは線形代数のメリットをあまり感じないかもしれません。しかし、入力が同時に50個や100個になってくると線形代数が大きなメリットを発揮します。
確率統計でデータの偏りやばらつきを整える
機械学習を行うには元となるサンプルデータが必要です。これを利用して数学的な観点からモデルを完成させるからです。
ただ、サンプルデータには偏りやばらつきがあると考えられます。必ずしも機械学習に適したサンプルデータだけが手に入るとは限りません。
そこで活用できるものが確率統計です。こちらを利用することによって、サンプルデータの偏りやばらつきを数学的に取り扱うことが可能です。以下では機械学習に利用される確率統計についてもご説明していきます。
確率統計とは~数学のおさらい~
確率と統計はそれぞれ別の学問です。ただ、多くの場合これらはひとつにまとめて考えられています。その方が処理しやすいという数学的な理由があります。
それそれがどのようなものであり、機械学習を数学の観点からどのように支えているのかもご説明します。
確率とは
数学的に確率を定義すると様々な前提条件を定義しなければなりません。ただ、そのような説明をすると内容が複雑になりすぎてしまいます。そのため今回は「想定している複数の出来事がどの程度発生するか」との度合いを確率として定義します。
「それぞれの出来事に対してどの程度発生するかの度合い」を確率変数と呼びます。変数と記載されると変動する数値のように思うかもしれませんが、基本的に確率を考えるにあたり確率変数は変動しません。例えばサイコロを転がす場合、1から6の目が出る確率変数は以下のとおりです。
| 値 | 確率 |
| 1 | 1/6 |
| 2 | 1/6 |
| 3 | 1/6 |
| 4 | 1/6 |
| 5 | 1/6 |
| 6 | 1/6 |
サイコロは基本的に6面ありそれぞれに1から6の数字が記載されています。そのため、どの数字も1/6の確率で出現しますので、確率変数は上記のようになります。
なお、上記のようなとりうる値とその時の確率を表にまとめたものを確率分布と呼びます。この確率分布には2つの条件があります。
ひとつめの条件が、記載されている確率の合計が「1」にならなければならないことです。取りうる全ての出来事を合計すると全体にならなければなりませんので、100%すなわち1にならなければならないのです。
ふたつめの条件が全ての確率が0以上の値であることです。確率はマイナスになることがありませんので、0以上の値で定義しなければなりません。なお、発生しないという出来事を表現するために、確率を0として定義することは問題ありません。
確率を定義することによって、その出来事がどれくらいの割合で起こる可能性があるのかを考えられます。出来事を確率的に判断することで、その出来事はたまたま発生したのか発生して当たり前であるのかを判断できます。機械学習においてはサンプルデータが必要となりますが、このデータには入力間違いなどで誤ったものが含まれている可能性があります。また、とんでもない能力を持った人がすごい記録を出した可能性もあります。そのような通常とは外れたと思われるデータを、発生する可能性から考慮するかどうか決めるのです。
統計とは
統計とは観測されたデータの数値や観測する事象そのもののことを指します。数学の世界ではもっぱら前半の意味を指し、観測されたデータの数値とそれらを加工して数学的な数値のことを指します。
統計にはいくつもの要素が存在しており、代表的なものでは平均・分散・標準偏差があります。それぞれについて簡単にご説明をしておきます。
平均とは観測されたデータの数値を合計し、合計した個数で割ったものの数値です。一般的にN個のデータの平均は以下のような式で表されます。
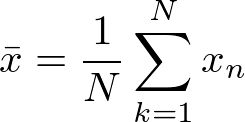
平均を求めることによって、そのデータの中心的な値・重心を理解できます。
続いて分散はデータが平均よりどの程度ばらついているのかを表す値です。データから平均を引き2乗した値の平均を計算します。数式では以下のとおりです。
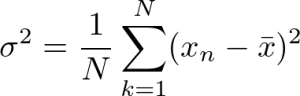
データが全体的に近い値を持っているのか遠い値を持っているのかを知る指標です。例えば平均よりも極端に大きなデータや極端に小さなデータがある場合は分散が大きくなります。
分散を利用することで機械解析に利用するデータのばらつきを評価できます。ばらつきの大きすぎるデータでは機械学習で期待するほどの数値が出ない可能性もあります。また、そもそも機械学習に利用するデータとして適切でない場合もあります。分散を利用してデータのばらつきを定量的に評価しなければならないのです。
最後に標準偏差とは分散の平方根を求めたものです。標準偏差はデータのばらつきが求めているものの、元のデータを二乗していますので単位も同時に二乗されてしまう問題があります。もちろんそのまま利用できないわけではありませんが、場合によってはやや不都合があります。
そこで分散の平方根をとると単位が元通りになります。つまり同じ単位で評価できるようになるのです。分散のやや使いにくい部分を解決したものが標準偏差なのです。
機械学習で利用される確率統計
条件付き確率
機械学習でよく使われる確率の考え方に条件付き確率があります。条件付き確率はその名の通り前提条件がついた確率のことです。高校数学で学習する範囲ですので、名前を聞いたことがある人は大半でしょう。
今まで確率の計算は全体の出来事から該当する出来事が起こる割合を計算するものでした。しかし、条件付き確率は全体の出来事から計算するのではなく、事前に条件を満たした出来事から該当する出来事が起こる割合を計算します。特定の出来事の中で起こる確率だけに注目した考え方です。
例えば「ある生徒が学校に傘を忘れた際、その日が雨である確率」といった条件確率を求めてみましょう。条件付き確率を求めるにあたりまずはそれぞれの物事が同時に起こる確率をしなければなりません。今回は以下のような確率で同時に起こると考えてみます。
| 天気が雨 | 天気が雨ではない | |
| 傘を忘れる | 0.05 | 0.50 |
| 傘を忘れない | 0.15 | 0.30 |
この確率を条件付き確率の本文に照らし合わせてみると以下の式と確率が導き出されます。
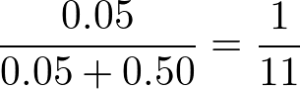
ここでは実際に数値を利用して計算しましたが、条件付き確率は以下の公式で表せます。
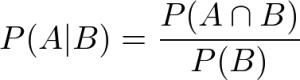
A|BはBの条件が満たされた際にAが起こる確率との意味です。数学的な記載ルールですので覚えるようにしておきましょう。また、今回は条件付き確率ですので前提としてAの条件が起こっている必要があります。その上でAとBの両方が起こっていると考えられますので、右のような式にも変形できます。
条件付き確率が計算できることで、機械学習の精度を上げることが可能です。特定の条件を満たしていることを踏まえると、多少飛び出したように見えるデータでも必要なものであるなどと判断ができます。
ベイズの定理
上記の条件付き確率では「ある条件が満たされている状態での確率」を求めました。しかし、「ある結果が得られた時にある条件が満たされていた確率」を求めたいこともあるでしょう。この時に利用されるものがベイズの定理です。
ベイズの定理を求めるにあたりわかりやすいものは、上記の条件付き確率の公式を使ったものです。この式を変形すると以下のようになります。
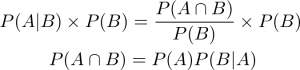
また、この公式はAとBの位置を逆にしても成り立ちます。つまりAの条件が成り立つときにBの条件も成り立つことを考えれば良いのです。これらの式をまとめると以下のような式が導き出されます。
![]()
これをベイズの定理と呼んでいます。条件が満たされていることを踏まえて物事が発生する確率や物事が発生した際に前提条件が満たされていた確率が求まります。
ベイズの定理や条件付き確率を利用することで「事前確率」と呼ばれるものが導かれます。これは機械学習によって導かれたモデルがどのような場合に成り立つかを判断するのに役立ちます。また、与えられたサンプルの中に特定の条件でのみ発生するような偏りのあるデータが無いかなどを判断するのにも利用できます。
機械学習で求められる数学は順を追って理解する
機械学習で求められる数学力は順を追って理解することが重要です。一つひとつの数学力も問われますが、段階を踏んで「なぜ機械学習で必要なのか」を意識しながら学んでいきましょう。
特に機械学習では王道のモデル→目的関数→微分→データの最適化といった学び方があります。この流れを意識して数学の知識を身につけるようにしていくと良いでしょう。