記事の要点
- 深層学習モデルに自作の物理特徴量を学習させたが、予測精度は向上しなかった
- 深層学習モデルは生の座標データから高度な物理概念を学習する能力を持っている
- 小手先の技術より、AIが持つ学習能力を利用し、そのポテンシャルを最大限に引き出すための「環境(モデル構造やデータの質)」を設計することが重要である
はじめに
株式会社エスタイルのなみーです。
近年、スポーツアナリティクス分野におけるAI活用は目覚ましい進化を遂げており、機械学習による選手の動き予測は、戦術立案での活用に大いに期待されています。本記事は、NFL(ナショナル・フットボール・リーグ)が主催し、プレイ中の選手の動きやプレイ結果を予測する精度を競う「NFL Big Data Bowl 2026」に参加し、精度向上を目指した奮闘記です。
GNNとTransformerを組み合わせた最新モデルに対して、「回転エネルギー」などの物理的特徴量を追加することで予測精度が向上するのか検証しました。結果として、人間の手による特徴量エンジニアリングと、深層学習による自動特徴抽出のどちらが優れているのか、興味深い知見が得られました。
執筆の背景
私が今回のコンペティションに参加しようと思ったきっかけは、社内のエンジニア教育制度「ESTYLE U」で開催された「機械学習エンジニアリング」の講義でした。普段の業務でもAI開発に携わっていますが、改めてデータ分析の基礎から応用までを体系的に学ぶ中で、講義の課題として参加したKaggleコンペティションという実戦形式の面白さに惹かれました。
その後、同僚から「開催中のKaggleのコンペに出てみないか」と誘いを受け、合計4名のチームとして参加しました。AIを開発・実装する上で、データの特性を理解し、仮説を立てて検証する「データ分析」のスキルを持っておくことは大きな強みになると思います。最新のモデルアーキテクチャを学ぶだけでなく、泥臭い試行錯誤を通じて技術力を底上げしたいという思いから、世界中のデータサイエンティストが競い合うNFL Big Data Bowlへの挑戦を決意しました。
説明:NFL Big Data Bowlとベースラインモデルの概要
NFL Big Data Bowlとは
NFL Big Data Bowlは、アメリカンフットボールのプロリーグであるNFLが主催する、スポーツデータ分析のコンペティションです。提供されるデータは非常にリッチで、試合中の全選手の座標、速度、加速度、向きなどが0.1秒刻みで記録されたトラッキングデータ(NGS: Next Gen Stats)が使用できます。
今回の課題は、プレイごとの選手の動きを予測することです。時系列データとしての分析と、選手間の相互作用(グラフ構造)としての分析の両面が必要となる、非常に難易度の高い課題でした。
ベースラインモデルの構造
今回、私たちがベースラインとして採用したのは、GNN(Graph Neural Network) と Transformer を組み合わせたハイブリッドモデルです。
本モデルの実装にあたっては、Kaggle上で公開されている以下のベースラインコードを参考にしました。
- Reference Code: NFL Big Data Baseline (Kaggle)
このモデルの最大の特徴は、「空間」と「時間」の両方を捉えるアーキテクチャにあります。
具体的には以下の処理を行っています。
- GNNによる空間情報の処理: 各選手をグラフ上のノードと見なし、選手間の距離や関係性を学習します。「誰が誰をブロックしているか」「近くに敵がいるか」といった、空間的な相互作用を捉えます。
- Transformerによる時系列情報の処理: GNNで抽出した特徴量を時系列データとしてTransformerに入力します。過去のフレームからの流れをAttention機構で捉えることで、次の動きを予測します。
アメフトの試合では、選手単独の動きだけでなく、「敵が近くにいるか」「味方がブロックしてくれているか」といった、選手間の関係性が極めて重要になります。GNNはこの「関係性」を処理するのに長けており、各選手をノード、選手間の距離をエッジとしてグラフ構造を学習します。
一方で、選手の動きは時間の経過とともに変化します。この時系列の変化を捉えるために、自然言語処理で圧倒的な成果を上げているTransformerを採用しました。過去のフレームからの動きの流れ(文脈)をAttention機構で捉え、未来の動きを予測します。
このベースラインモデルの時点で、検証データに対するRMSE(平均二乗誤差の平方根)は 0.861 という高いスコアを出していました。ここからさらに精度を上げるために、私たちは「物理学」の理論をモデルに組み込むことに挑戦しました。
実装:物理特徴量によるAI強化計画
仮説:AIは「物理」を理解していない?
ベースラインモデルは優秀ですが、入力されているデータは主に「座標 (x, y)」「速度 (s)」「加速度 (a)」「向き (dir)」といった基本的な数値だけでした。
しかし、実際のアメフトの動きには複雑な物理法則が働いています。例えば、急激に方向転換をする際、選手には強い負荷(回転エネルギー)がかかり、減速を余儀なくされます。また、ボールを持っている選手はエンドゾーン(ゴール)を目指しますが、ディフェンダーはボールキャリアの未来位置を予測して動きます。
そこで、私たちは次のような仮説を立てました。
「AIは単なる数値の羅列を見ているだけで、慣性やエネルギー保存則といった物理的な制約までは理解しきれていないのではないか? 人間が計算式を使って物理的な特徴量(ヒント)を与えてあげれば、AIはもっと賢くなるはずだ」
この仮説に基づき、以下の特徴量を実装し、モデルに追加することにしました。
1.プレイ方向の標準化(Play Direction Normalization)
データの学習効率を上げるための前処理です。アメフトのフィールドは左右対称であるため、すべてのプレイを「左から右」への攻撃方向に統一(座標変換)することで、データのばらつきを減らし、モデルがパターンを学習しやすくなると考えました。
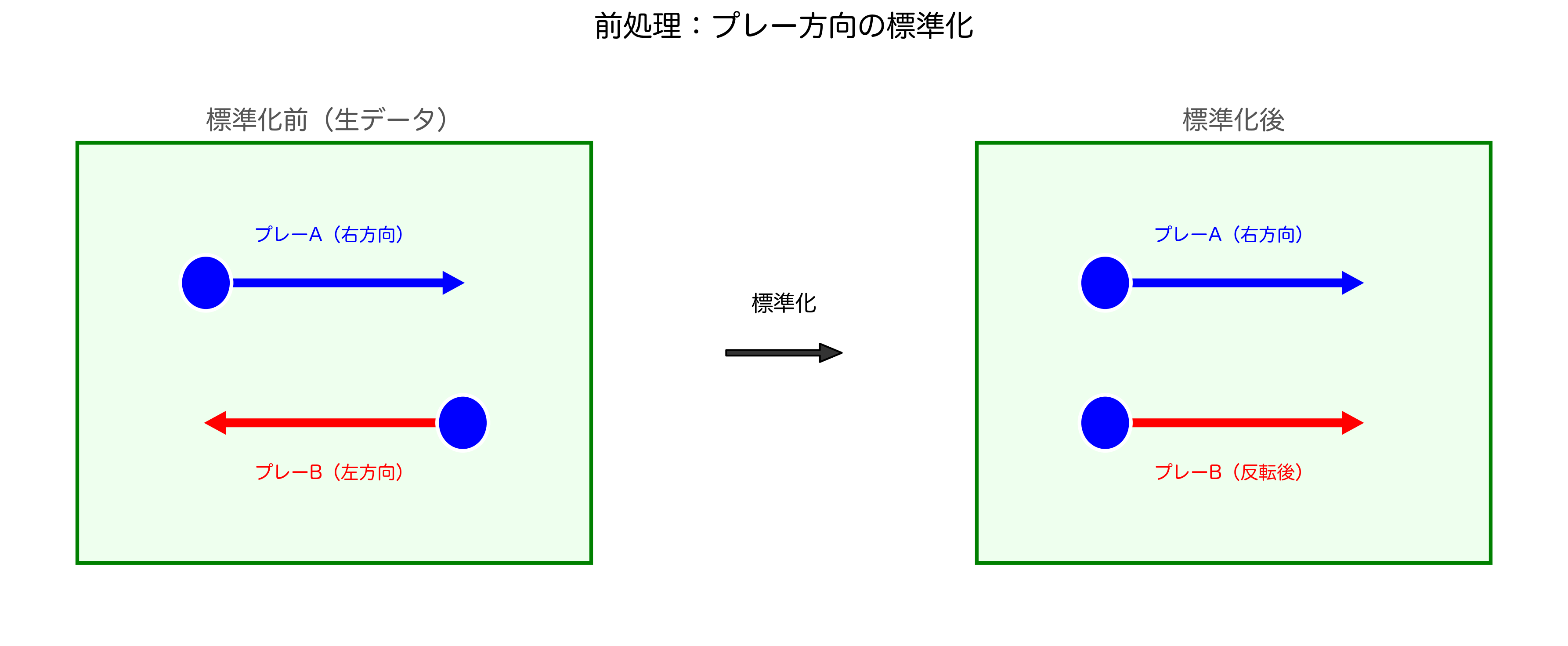
プレイ方向の標準化のイメージ図
2.回転エネルギー(Rotational Energy)
速度と方向転換の激しさ(角速度のようなもの)を掛け合わせた値です。これが大きいほど、選手は急激なターンを行っており、次の動きに制約がかかるはずです。
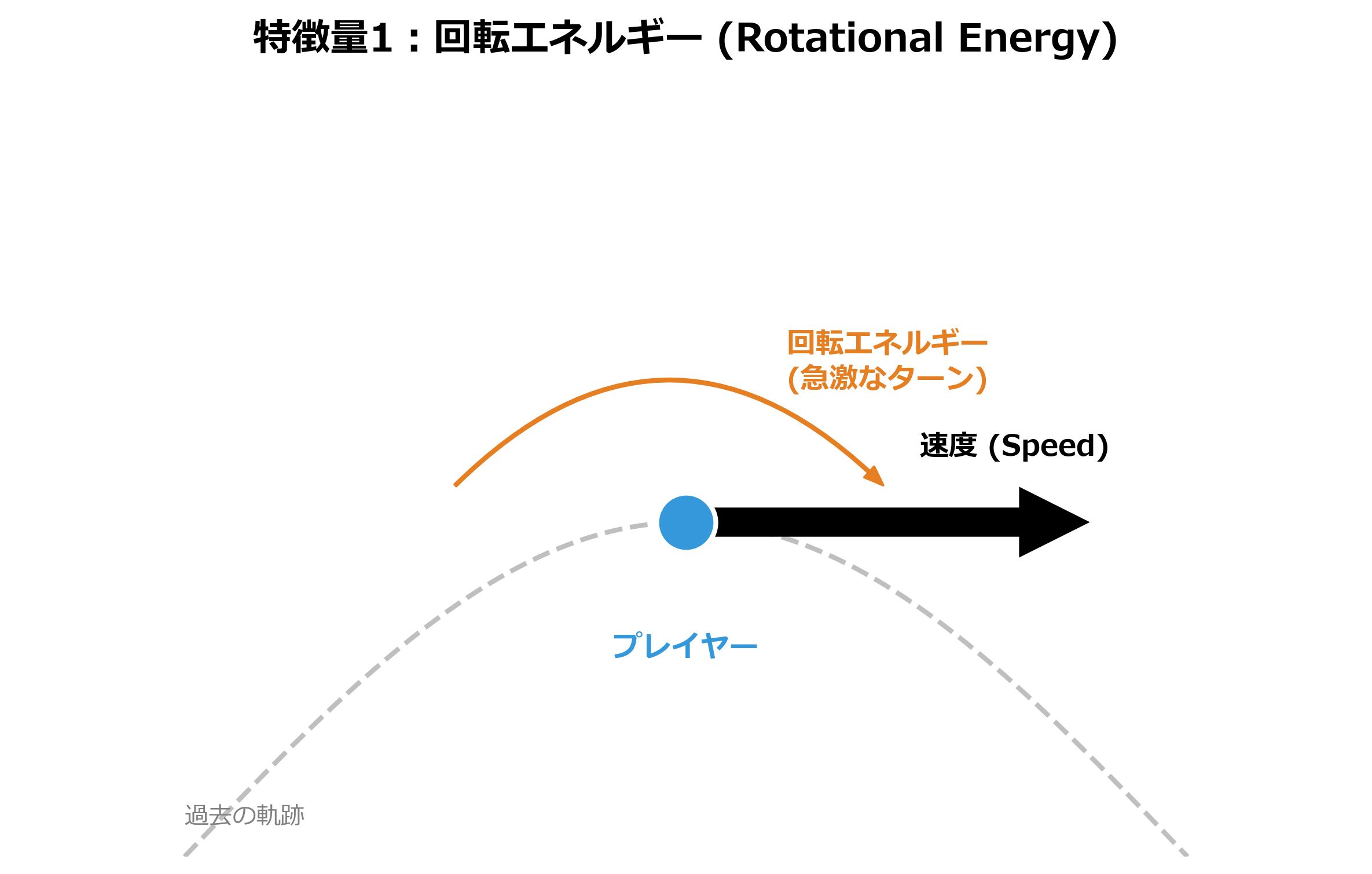
回転エネルギーのイメージ図
3. ベクトル分解(Vector Decomposition)
選手の身体の向きに対する、進行方向(Forward)と横方向(Lateral)への速度成分です。カニ走りをしているのか、前進しているのかを明確にします。
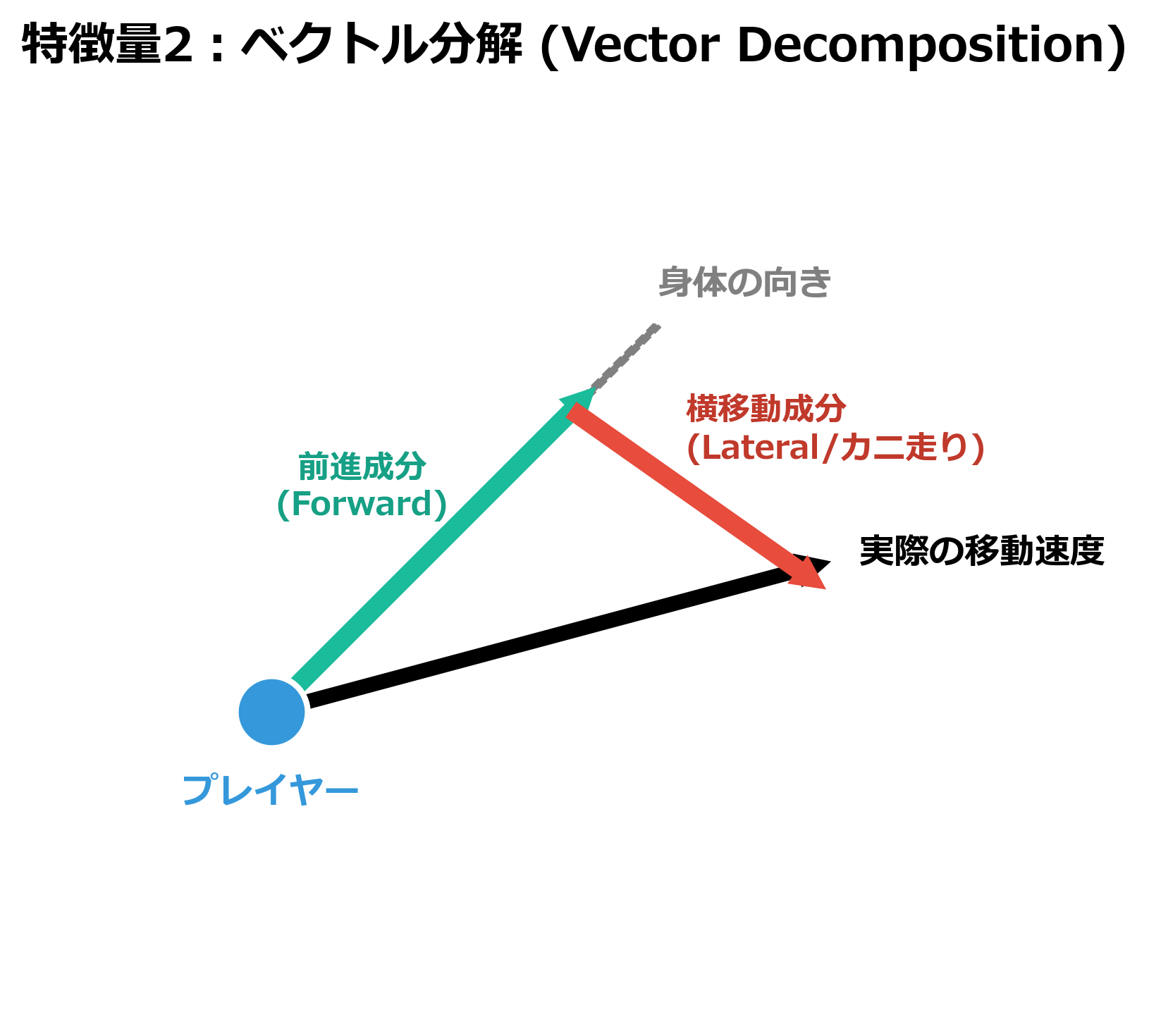
ベクトル分解のイメージ図
4.フィールド絶対位置(Field Position)
サイドラインやエンドゾーンまでの距離です。「サイドライン際ではアウトにならないように動く」といった、戦術的なバイアスを学習させる狙いです。
フィールド絶対位置のイメージ図
5.その他、相対関係・時系列変化(Interactions & Deltas)
上記に加え、ボールや最も近い敵選手との相対角度・距離、および直前フレームからの速度・加速度の変化量なども、基本的なコンテキスト情報としてコードに含めています。
相対関係・時系列変化のイメージ図
- 実装コードとその使用方法
これらの計算処理をまとめたコードを、今回は utils_nfl.py という独立したモジュールとして実装しました。 このモジュールを、メインの学習スクリプト(Notebook等)から読み込んで使用します。
※具体的な実装コードは、記事の最後にある Appendix(参考コード) に掲載しています。
実験
実験1:プレイ方向の「標準化」の罠
まず最初に行った実験では、データの前処理としてプレイ方向の標準化と4種類の物理特徴量の追加を行いました。プレイ方向の標準化には、確固たる理論的な狙いがありました。
アメフトのフィールドは幾何学的に完全な左右対称です。物理学の視点で見れば、左から右への攻撃も、右から左への攻撃も、選手にかかる重力や慣性の法則は全く変わりません。そこで私たちは、「フィールドの対称性を利用して入力空間を圧縮すれば、モデルの汎化性能が劇的に向上するはずだ」という仮説を立てました。 具体的には、全てのプレイを座標変換によって「左から右」への攻撃方向に標準化しました。これにより、モデルが学習すべきパターン数が実質半分になり、データのスパース性(疎らさ)を解消できると考えたのです。
「これでデータ量は実質2倍、力学的特徴量も追加済み。スコアが跳ね上がるのは間違いない。」
チーム全員がそう確信して結果を待ちました。
しかし、出力されたスコアを見た瞬間、私たちは言葉を失いました。
RMSE: 1.084
ベースラインの 0.861 から、改善どころか大幅に悪化してしまったのです。 なぜ、物理的・幾何学的に正しいはずのアプローチが裏目に出たのか? ログを詳細に解析し、私たちはアメフトというスポーツの特異性を見落としていたことに気づきました。
それは、「幾何学的な対称性」と「戦術的な非対称性」の乖離です。
確かにフィールドの形状は対称ですが、実際の試合における「自陣1ヤード地点(セーフティのリスクがある極限状態)」と「敵陣1ヤード地点(タッチダウン直前のチャンス)」では、選手の心理状態や採用される戦術(プレイコール)が根本的に異なります。 全てのプレイを同じ向きに畳み込んでしまったことで、モデルは「今、自分たちがフィールドの『どのエリア』で戦っているのか」という、勝敗を分ける最も重要な文脈(Context)を喪失してしまったのです。
良かれと思って行った高度な標準化処理が、実は「戦術的な絶対座標」という極めて重要な情報を破壊するノイズとなっていた。これが、私たちが最初に直面した大きな壁でした。
実験2:純粋な物理特徴量の検証
気を取り直して、2回目の実験です。今回は「プレイ方向の標準化」を廃止し、データの向きはそのままにしました。つまり、ベースラインと同じ条件(プレイ方向の標準化なし)に戻し、純粋に「4種の物理特徴量」だけを追加した状態で再学習を行いました。
なお、この実験では「特徴量そのものの効果」を公平に測定するため、学習率やバッチサイズ、モデルのレイヤー数といったハイパーパラメータは、ベースラインから一切変更していません。 変数を「追加した特徴量の有無」のみに絞った、厳密なA/Bテストです。
「これでプレイ方向の標準化の悪影響は消えた。物理の知識を得たAIは、ベースラインを超えるはずだ。」
そう信じて待った結果がこちらです。
RMSE: 0.864
ベースラインは 0.861 です。
悪化は止まりましたが、スコアは戻っただけ。むしろ、わずかに負けています。学習曲線をモニタリングしていても、ベースラインとの有意な差は見られず、淡々と学習が進んで終わりました。 苦労しながら計算式を実装し、物理的な意味を持たせた特徴量を追加したにもかかわらず、精度は全く向上しませんでした。
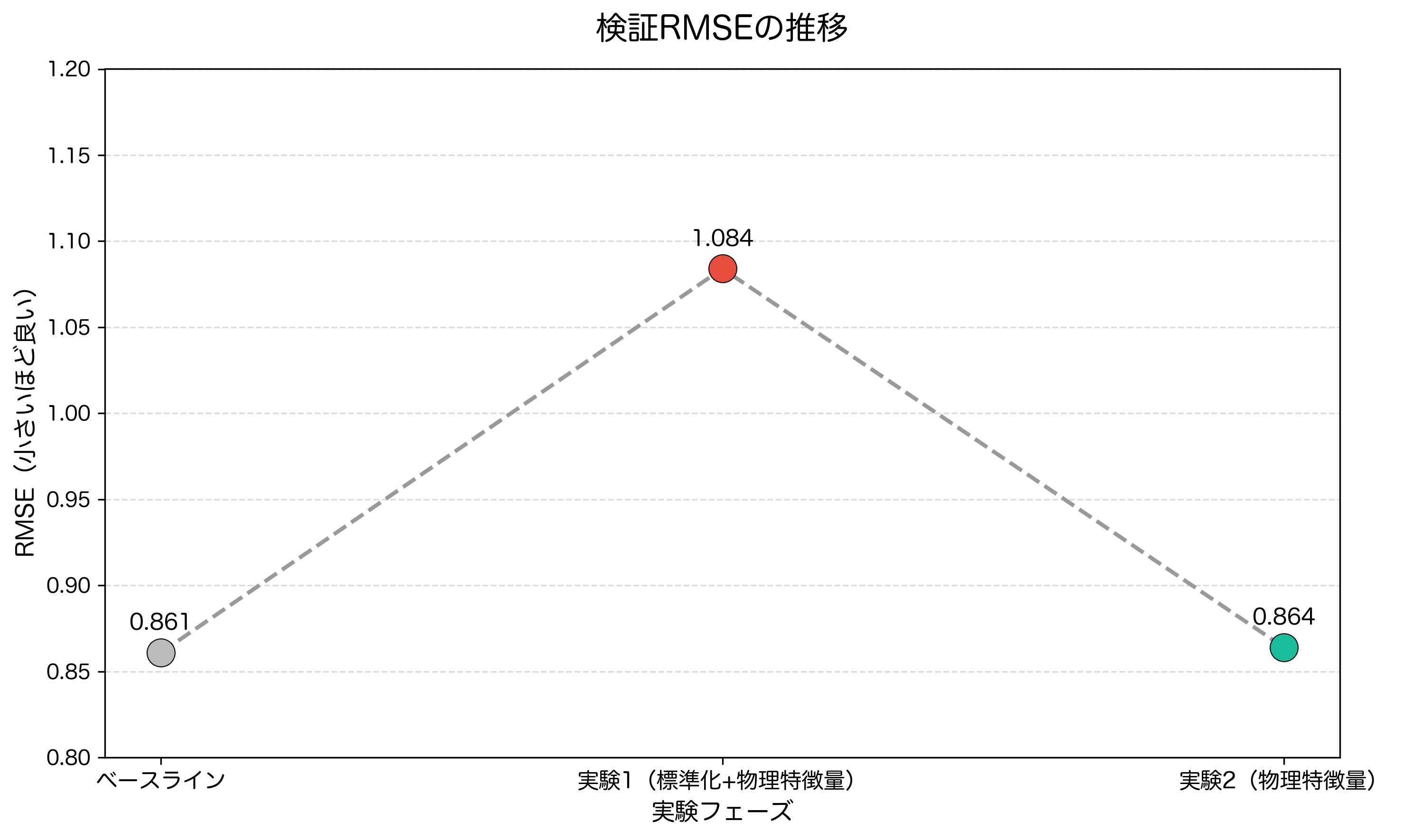
ベースラインと二つの実験のRMSE結果
このように、私たちは「プレイ方向の標準化」と「物理特徴量の追加」という2つのアプローチで精度の改善を試みましたが、残念ながらいずれもベースライン(RMSE: 0.861)を上回る成果を上げることはできませんでした。
では、なぜこれらのアプローチは機能しなかったのか? その根本的な原因を技術的な視点から深掘りします。
まとめ/今後の展望
なぜAIは賢くならなかったのか?
今回の実験で得られた結果は、ある意味で衝撃的でした。人間が良かれと思って与えた物理的なヒントは、最新の深層学習モデルにとっては無意味だったのです。この現象について、技術的な観点から以下の3つの理由が考えられます。
- 情報の等価性(Information Equivalence)
私たちが追加した「回転エネルギー」や「移動ベクトル」といった特徴量は、元データにある「速度」「加速度」「向き」などの変数を四則演算で組み合わせたものであり、情報理論的に言えば、新しい外部情報は一つも追加されていなかったのです。
- ニューラルネットワークの「万能近似能力」
ここが最も重要な点です。多層パーセプトロン(MLP)やTransformerといった深層学習モデルは、「万能近似定理(Universal Approximation Theorem)」により、理論上あらゆる関数を近似できることが知られています。
私たちが追加した「回転エネルギー」は、元データである「速度」と「角度変化」の掛け算に過ぎません。モデルは学習の過程で、生の座標データの非線形変換を通じて、この「速度×角度変化」に相当する重要なパターンを、隠れ層の重みとしてすでに獲得していたと考えられます。
実際、今回の実験でスコアが向上しなかったことは、「人間が計算した物理特徴量が、モデルにとっては既知の冗長な情報であった」という事実を強く裏付けています。
- 冗長性とノイズ
モデルがすでに内部で計算済み(あるいは計算可能)な情報を、人間が改めて計算して入力として与えることは、モデルにとっては「同じことを2回言われる」ようなものです。これは情報の冗長性を生み、場合によってはモデルのパラメータ最適化を邪魔するノイズになり得ます。今回のRMSEの微増(悪化)は、まさにこの冗長性が原因だったと考えられます。
結論
「AIに物理法則を教える」という私たちのアプローチは、AIの能力を過小評価した、ある種の「お節介」だったのかもしれません。最新のモデルは、大量のデータさえあれば、人間が手計算で作るレベルの特徴関係を自力で近似し、データに適合(Fit)する能力を持っています。 したがって、今後の特徴量エンジニアリングにおいては、既存データの加工に時間を費やすのではなく、モデルが自力では観測できない「外部情報(ドメイン固有の制約や、データに含まれないコンテキスト)」をいかに追加するかに注力すべきだという教訓を得ました。
今後の展望
今回のコンペティションを通じて、特徴量エンジニアリングの在り方について深く考えさせられました。かつての機械学習(勾配ブースティングなど)では、人間がいかに気の利いた特徴量を作るかが勝負でしたが、高度な深層学習モデルにおいては、その常識が通用しない場面が増えています。
今後は、小手先の特徴量計算に時間を割くのではなく、以下のようなアプローチに注力していきたいと考えています。
- モデルアーキテクチャの改善: データが持つグラフ構造や時系列情報を、より効率的に捉えられるモデル構造を探求する。
- データの質の向上: 特徴量を増やすのではなく、ノイズの除去や、モデルが苦手とするエッジケースのデータを集中的に学習させる。
AIが持つ圧倒的な学習能力を利用し、そのポテンシャルを最大限に引き出すための「環境(モデル構造やデータの質)」を設計する。それこそが、これからの深層学習時代において、私たち人間に求められる役割なのではないかと考えさせられる良い経験になりました。
物理学的な理論をモデルに埋め込むことに固執した今回の反省と、モデルの挙動から得られたこの知見を活かし、次回のコンペではさらなる高みを目指したいと思います。
Appendix(参考コード)
import numpy as np
import pandas as pd
FIELD_X = 120.0
FIELD_Y = 53.3
# =========================================================
# 共通ユーティリティ
# =========================================================
def angle_diff_deg(a: pd.Series, b: pd.Series) -> pd.Series:
"""
2つの角度 a, b(度)から、a - b の差を -180〜180 にプレイ方向の標準化して返す。
"""
diff = a - b
diff = (diff + 180.0) % 360.0 - 180.0
return diff
# =========================================================
# 1. 方向プレイ方向の標準化(left → right にそろえる)
# =========================================================
def normalize_play_direction(df: pd.DataFrame) -> pd.DataFrame:
"""
play_direction が 'left' のプレイを、右方向攻撃ベースに反転する。
- x, y
- dir(移動方向)
- o(身体の向き)
- ball_land_x, ball_land_y
を反転させる。
学習前処理・推論前処理の両方で共通して使う想定。
"""
df = df.copy()
if "play_direction" not in df.columns:
# 何もできないのでそのまま返す
return df
left_mask = df["play_direction"] == "left"
# 位置の反転
df.loc[left_mask, "x"] = FIELD_X - df.loc[left_mask, "x"]
df.loc[left_mask, "y"] = FIELD_Y - df.loc[left_mask, "y"]
# 向き・移動方向(180度回転)
if "dir" in df.columns:
df.loc[left_mask, "dir"] = (df.loc[left_mask, "dir"] + 180.0) % 360.0
if "o" in df.columns:
df.loc[left_mask, "o"] = (df.loc[left_mask, "o"] + 180.0) % 360.0
# ボール着地点
if "ball_land_x" in df.columns:
df.loc[left_mask, "ball_land_x"] = FIELD_X - df.loc[left_mask, "ball_land_x"]
if "ball_land_y" in df.columns:
df.loc[left_mask, "ball_land_y"] = FIELD_Y - df.loc[left_mask, "ball_land_y"]
# 以後は right 固定として扱えるように上書き
df["play_direction"] = "right"
return df
# =========================================================
# 2. 方向を元に戻す(推論用:leftプレイには逆変換をかける)
# =========================================================
def revert_play_direction(
df_pred: pd.DataFrame,
original_play_direction: pd.Series
) -> pd.DataFrame:
"""
normalize_play_direction 後の座標系で予測された x, y を、
元の play_direction(left/right)にもどすための関数。
df_pred: 予測結果を持つ DataFrame(少なくとも x, y を含む)
original_play_direction: 各行に対応する元の play_direction(left or right)
※学習時には不要で、推論時にだけ使用する想定。
"""
df_pred = df_pred.copy()
# Series を align させる
play_dir = original_play_direction.reindex(df_pred.index)
left_mask = play_dir == "left"
# left プレイは再度反転させて元に戻す
df_pred.loc[left_mask, "x"] = FIELD_X - df_pred.loc[left_mask, "x"]
df_pred.loc[left_mask, "y"] = FIELD_Y - df_pred.loc[left_mask, "y"]
return df_pred
# =========================================================
# 3. 物理・時系列・相互作用特徴の追加
# =========================================================
def add_physics_and_interaction(df: pd.DataFrame) -> pd.DataFrame:
"""
上司ベースの特徴量 +
・時系列Δ特徴(dx, dy, ds, da)
・前進/横方向(v_forward, v_lateral とその差分)
・ボール方向との相対角度
・最も近い敵との相対ベクトル(opp_x, opp_y, opp_s がある場合)
などを追加する。
前提:
- df は normalize_play_direction 済み(全部 right 攻撃)
- カラム例:
['game_id', 'play_id', 'nfl_id', 'x', 'y', 's', 'a', 'dir', 'o',
'player_side', 'player_role', 'ball_land_x', 'ball_land_y', ...]
"""
df = df.copy()
gcols = ["game_id", "play_id", "nfl_id"]
# ---------------------------------------------------------
# 0. 前フレーム情報(Δ計算用)
# ---------------------------------------------------------
for col in ["x", "y", "s", "a", "dir"]:
prev_col = f"prev_{col}"
df[prev_col] = df.groupby(gcols)[col].shift(1)
df[prev_col] = df[prev_col].fillna(df[col])
# ---------------------------------------------------------
# 1. フィールド境界関連
# ---------------------------------------------------------
df["dist_to_sideline_y"] = np.minimum(df["y"], FIELD_Y - df["y"])
df["dist_to_endzone_x"] = np.minimum(df["x"], FIELD_X - df["x"])
# ---------------------------------------------------------
# 2. 角度キネマティクス(ターンの鋭さ)
# ---------------------------------------------------------
df["dir_change_rate"] = angle_diff_deg(df["dir"], df["prev_dir"])
df["rotational_energy"] = df["s"] * np.abs(df["dir_change_rate"])
# ---------------------------------------------------------
# 3. ボールへの到達時間(dist_to_ball があるなら)
# ---------------------------------------------------------
if "dist_to_ball" in df.columns:
df["eta_to_ball"] = df["dist_to_ball"] / (df["s"] + 1e-6)
else:
df["eta_to_ball"] = np.nan
# ---------------------------------------------------------
# 4. 時系列Δ特徴(位置・速度・加速度)
# ---------------------------------------------------------
df["dx"] = df["x"] - df["prev_x"]
df["dy"] = df["y"] - df["prev_y"]
df["ds"] = df["s"] - df["prev_s"]
df["da"] = df["a"] - df["prev_a"]
df["step_dist"] = np.sqrt(df["dx"] ** 2 + df["dy"] ** 2)
# ---------------------------------------------------------
# 5. 前方向 / 横方向ベクトルとその変化
# ---------------------------------------------------------
rad_dir = np.deg2rad(df["dir"])
df["v_forward"] = df["s"] * np.cos(rad_dir) # 攻撃方向成分
df["v_lateral"] = df["s"] * np.sin(rad_dir) # 横方向成分
df["prev_v_forward"] = df.groupby(gcols)["v_forward"].shift(1)
df["prev_v_lateral"] = df.groupby(gcols)["v_lateral"].shift(1)
df["prev_v_forward"] = df["prev_v_forward"].fillna(df["v_forward"])
df["prev_v_lateral"] = df["prev_v_lateral"].fillna(df["v_lateral"])
df["dv_forward"] = df["v_forward"] - df["prev_v_forward"]
df["dv_lateral"] = df["v_lateral"] - df["prev_v_lateral"]
# ---------------------------------------------------------
# 6. ボール方向との相対角度
# ---------------------------------------------------------
if {"ball_land_x", "ball_land_y"}.issubset(df.columns):
df["angle_to_ball"] = np.degrees(
np.arctan2(df["ball_land_y"] - df["y"], df["ball_land_x"] - df["x"])
)
df["dir_diff_ball"] = angle_diff_deg(df["dir"], df["angle_to_ball"])
else:
df["angle_to_ball"] = np.nan
df["dir_diff_ball"] = np.nan
# ---------------------------------------------------------
# 7. 近傍敵との相互作用(opp_* があれば)
# ---------------------------------------------------------
# gnn_opp_dmin があればプレッシャー指標
if "gnn_opp_dmin" in df.columns:
df["pressure_index"] = 1.0 / (df["gnn_opp_dmin"] + 0.5)
df["speed_under_pressure"] = df["s"] * df["pressure_index"]
else:
df["pressure_index"] = np.nan
df["speed_under_pressure"] = np.nan
# 最も近い敵の座標がある場合の相対ベクトル
if {"opp_x", "opp_y"}.issubset(df.columns):
df["opp_dx"] = df["opp_x"] - df["x"]
df["opp_dy"] = df["opp_y"] - df["y"]
df["opp_dist"] = np.sqrt(df["opp_dx"] ** 2 + df["opp_dy"] ** 2)
df["opp_angle"] = np.degrees(np.arctan2(df["opp_dy"], df["opp_dx"]))
df["opp_dir_diff"] = angle_diff_deg(df["opp_angle"], df["dir"])
else:
df["opp_dx"] = df["opp_dy"] = df["opp_dist"] = np.nan
df["opp_angle"] = df["opp_dir_diff"] = np.nan
if "opp_s" in df.columns:
df["rel_speed_to_opp"] = df["s"] - df["opp_s"]
else:
df["rel_speed_to_opp"] = np.nan
# ---------------------------------------------------------
# 8. プレイ文脈(簡易版:攻撃/守備の平均速度)
# ---------------------------------------------------------
# player_side を使うので、存在しないならスキップ
if "player_side" in df.columns:
# transform を使うときは side ごとにマスクしてから groupby したほうが安全
off_mask = df["player_side"] == "Offense"
def_mask = df["player_side"] == "Defense"
df["offense_speed_mean"] = np.nan
df["defense_speed_mean"] = np.nan
df.loc[off_mask, "offense_speed_mean"] = (
df[off_mask]
.groupby(["game_id", "play_id"])["s"]
.transform("mean")
)
df.loc[def_mask, "defense_speed_mean"] = (
df[def_mask]
.groupby(["game_id", "play_id"])["s"]
.transform("mean")
)
return df
# =========================================================
# 4. 便利ヘルパー(学習時などに一発で処理したい場合)
# =========================================================
def normalize_and_add_features(df: pd.DataFrame) -> pd.DataFrame:
"""
1. left/right の方向プレイ方向の標準化
2. 物理 + 時系列 + 相互作用特徴の追加
をまとめて行うヘルパー。
"""
df_norm = normalize_play_direction(df)
df_feat = add_physics_and_interaction(df_norm)
return df_feat